决策树算法详解与python实现：ID3和CART

发表于 | 分类于 |
字数统计: 2,937 | 阅读时长 ≈ 12

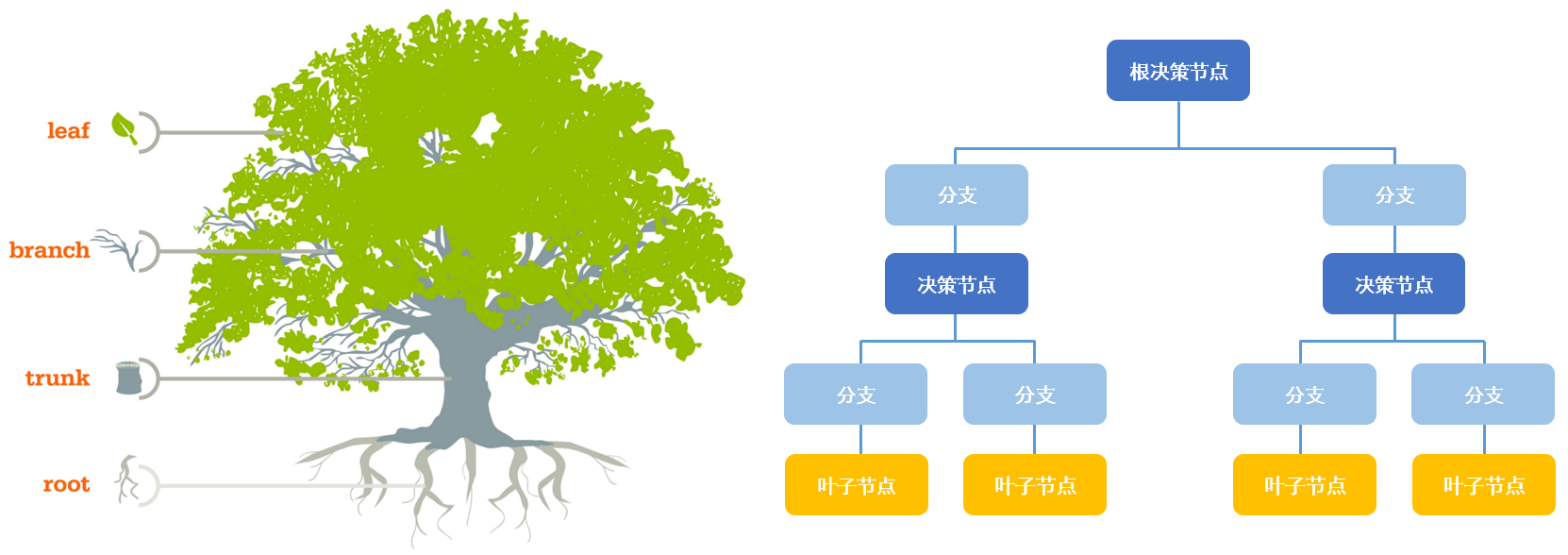
摘要 决策树是一种基本的分类与回归方法，本文主要讨论用于分类的决策树，决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程，它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布，其主要优点是模型具有可读性，分类速度快。学习时，利用训练数据，根据损失函数最小化原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。决策树学习通常包括三个步骤：特征选择、决策树的生成以及决策树的修剪。本文将主要讲解ID3和CART算法的原理和实现细节。

avatar

文章概览

  • ID3算法
    • 特征选择
    • 决策树的生成
    • ID3算法的缺陷
    • C4.5算法对ID3算法的改进
  • CART算法
    • 特征选择
    • 决策树生成
    • 剪枝

ID3算法

  ID3算法是由澳大利亚计算机科学家Ross Quinlan提出的，它是构建决策树中一种非常重要的算法。在设计算法的过程中，它首次采用了信息增益准则来进行特征选择，这很大程度上推动了决策树算法的发展。

特征选择

  我们可以将决策树看作是if- then规则的集合，使用决策树模型进行预测的过程就相当于对if - then规则进行判断，那我们可以想到如果if -then规则越多，也就是决策树越复杂，那么预测所需要的时间越长，所以为了不断优化决策树的决策过程，我们需要合理的构建决策树，那么如何来选择if - then的决策规则至关重要。

  在ID3算法中，我们通过信息增益作为决策规则。信息增益 = 信息熵 - 条件熵，信息熵代表随机变量的不确定度，条件熵代表在一定条件下，随机变量的复杂度，所以信息增益表示在一定条件下信息复杂度减少的程度。信息增益越大说明该决策规则的区分度越高，在构建决策树时，我们选取信息增益最大的特征作为决策规则。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def emp_entropy(y_data):
    '''
    emp_entropy函数的主要功能是计算数据集的经验熵
    :param y_data: 数据集的类别
    :return: 返回数据集的经验熵
    '''
    count = {}
    emp = 0.0
    m = len(y_data)
    for y in y_data:
        if y in count:
            count[y] += 1
        else:
            count[y] = 1
    for i in count.keys():
        info = (1.0 * count[i] / m)
        emp = emp + info * math.log(info,2)
    return emp

emp_entropy函数的主要功能是计算数据集合的经验熵，经验熵的计算公式可以参考《统计学习方法》，同样，下面涉及到条件熵、信息增益的计算公式也可参考本书。代码中字典count的主要作用是统计数据集中不同类别出现的次数，emp即是信息增益。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def emp_cond_entropy(x_data,y_data,feature):
    '''
    emp_cond_entropy函数的主要作用是计算经验条件熵
    :param x_data: 数据集
    :param y_data: 数据集类别
    :param feature: 数据集特征特征
    :return: 数据集的经验条件熵
    '''
    count_y = {}
    emp_cond = 0.0
    m = len(y_data)
    fea = x_data[:,feature]
    for i in range(len(fea)):
        if fea[i] in count_y:
            count_y[fea[i]].append(y_data[i])
        else:
            count_y.setdefault(fea[i])
            count_y[fea[i]] = []
            count_y[fea[i]].append(y_data[i])
    for e in count_y.keys():
        l = len(count_y[e])
        emp_cond = emp_cond + (1.0 * l / m) * emp_entropy(count_y[e])
    return emp_cond

emp_cond_entropy函数的主要作用是计算经验条件熵，fenture表示数据的某一维特征，对于离散性特征（ID3算法不能处理连续型特征）来讲，特征的取值有多个，这里的count_y就是来统计该特征中不同取值的数据分布情况，列表fea表示的即是该数据集中该特征对应的值，emp_cond表示的是将该特征作为决策规则时的条件熵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def choose_feature(x_data,y_data):
    '''
    choose_feature函数的主要作用是从数据集中选择信息增益最大的特征
    :param x_data: 数据集
    :param y_data: 数据集类别
    :return: 信息增益最大的特征
    '''
    n = np.size(x_data,1)
    count = []
    emp = emp_entropy(y_data)
    for i in range(n):
        emp_cond = emp_cond_entropy(x_data,y_data,i)
        count.append(emp - emp_cond)
    feature = count.index(min(count))
    return feature

choose_feature函数的主要作用是从数据集中选择信息增益最大的特征，算法的思路就是对数据集进行遍历，计算每一个特征的信息增益，返回信息增益最大的特征。（由于在计算经验熵的过程中没有添加负号，所以我这里取的是负数的最小值，也就是正数的最大值）

决策树的生成

  特征树的生成过程其实是一个递归过程，我们首先选择一个特征，作为根结点，根据根结点的不同取值，将数据集分为几个不同的部分，同时将该特征从数据集中删除。然后再对这几个不同的部分进行同样的操作，直到数据集类别相同或者没有特征为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def create_tree(x_data,y_data,feature_list_data):
    '''
    create_tree函数的主要作用是构建决策树
    :param x_data:
    :param y_data:
    :param feature_list:
    :return: 返回决策树
    '''
    feature_list = feature_list_data[:]
    if is_all_same(y_data):
        return y_data[0]
    if len(x_data) == 0:
        return node_classfy(y_data)
    feature = choose_feature(x_data,y_data)
    node_name = feature_list[feature]
    tree = {node_name:{}}
    del feature_list[feature]
    count_x,count_y = feature_split(x_data,y_data,feature)
    for i in count_x.keys():
        fealist = feature_list[:]
        count_x_del = del_feature(count_x[i],feature)
        tree[node_name][i] = create_tree(count_x_del,count_y[i],fealist)
    return tree

feature_list的作用是复制feature_list_data，因为后面要进行删除操作，我们要保证删除操作只能影响函数内部变量，不能对函数的实参造成影响。我们生成的决策树保存在tree字典中，每执行一次递归操作，相当于将当前特征作为一个字典的key，递归操作返回的即是一个子树（即字典）。

ID3算法的缺陷

  通过对ID3算法进行分析，我们可以知道，ID3算法主要存在以下缺陷：

  • ID3没有考虑连续型特征，数据集的特征必须是离散型特征
  • ID3算法采用信息增益大的特征优先建立决策树的结点，但是再计算信息增益的过程中我们发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大
  • ID3没有对缺失值情况进行处理，现实任务中常会遇到不完整的样本，即样本的某些属性值缺失。
  • 没有考虑过拟合问题

C4.5算法对ID3算法的改进

  C4.5算法是对ID3算法存在的缺陷进行改进的一种算法，它通过将连续特征离散化来解决ID3算法不能处理离散型数据的问题（这个会在后面的CART算法中讲到）；通过引入信息增益比来解决信息增益的缺陷；通过增加剪枝操作来解决过拟合的问题。

CART算法

  CART算法是一种应用广泛的决策树算法，它的基本流程与C4.5算法类似，它既可以应用于回归任务，也可以应用于分类任务（这里主要讲解分类树），需要注意的是CART算法生成的决策树是二叉树，而ID3和C4.5算法生成的决策树不一定是二叉树。

特征选择

  CART算法的决策规则由基尼指数决定，选择基尼指数最小的特征及其切分点作为最优特征和最优切分点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def Gini_index(y_data):
    '''
    Gini_index函数的主要作用是计算数据集的基尼指数
    :param y_data: 数据集类别
    :return: 返回基尼指数
    '''
    m = len(y_data)
    count = {}
    num = 0.0
    for i in y_data:
        if i in count:
            count[i] += 1
        else:
            count[i] = 1
    for item in count.keys():
        num = num + pow(1.0 * count[item] / m,2)
    return (1.0-num)

在前面提到过ID3算法只能处理离散型特征，而CART算法既能处理离散型特征，又能处理连续型特征。CART算法处理连续型特征的方法与C4.5算法类似，都是将连续特征离散化，即将连续特征的所有取值进行排序，然后计算相邻取值的平均值作为切分点，在以此计算基尼指数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
ef Gini_D_A(x_data,y_data,feature):
    '''
    Gini_D_A函数的主要作用是计算某一离散特征各个取值的基尼指数，选取最优切分点
    :param x_data: 数据集合
    :param y_data: 数据集类别
    :param feature: 特征
    :return: 该特征的最优切分点
    '''
    Gini_data = list(x_data[:,feature])
    y_data = list(y_data[:])
    m = len(Gini_data)
    Gini = {}
    classfy_data = {}
    for e in range(m):
        if Gini_data[e] not in classfy_data:
            classfy_data[Gini_data[e]] = []
        classfy_data[Gini_data[e]].append(y_data[e])
    for item in classfy_data.keys():
        l1 = len(classfy_data[item])
        r = y_data[:]
        for i in classfy_data[item]:
            r.remove(i)
        l2 = len(r)
        num = 1.0 * l1 / m * Gini_index(classfy_data[item]) + 1.0 * l2 / m * Gini_index(r)
        Gini[item] = num
    sor = sorted(Gini.items(), key=operator.itemgetter(1))
    return sor[0]

def Gini_continuous(x_data,y_data,feature):
    '''
    Gini_continous函数的主要作用是计算某一连续特征各个取值的基尼指数，选取最优切分点
    :param x_data: 数据集合
    :param y_data: 数据集类别
    :param feature: 特征
    :return: 该特征的最优切分点
    '''
    Gini_data = list(x_data[:,feature])
    m = len(Gini_data)
    y_data = list(y_data[:])
    sort_data = sorted(Gini_data)
    Gini = {}
    split_point = []
    for i in range(m-1):
        num = (sort_data[i] + sort_data[i+1]) / 2.0
        split_point.append(num)
    for e in split_point:
        count_y = {0:[],1:[]}
        for k in range(m):
            if Gini_data[k] <= e:
                count_y[0].append(y_data[k])
            else:
                count_y[1].append(y_data[k])
        cal = 1.0 * len(count_y[0]) / m * Gini_index(count_y[0]) + 1.0 * len(count_y[1]) / m * Gini_index(count_y[1])
        Gini[e] = cal
    sor = sorted(Gini.items(), key=operator.itemgetter(1))
    return sor[0]

当数据集中同时含有离散型变量和连续型变量时，进行特征选择就稍微有些复杂了，以下便是特征选择的代码,这里需要注意的是对不同类型特征的标识和对计算基尼指数时返回值的统一处理。dis_or_con是一个列表，用来标识特征是连续型还是离散型，0表示离散，1表示连续。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def choose_feature(x_data,y_data,dis_or_con):
    '''
    choose_feature函数的主要作用是从各个特征的各个切分点中选择基尼指数最小的切分点
    :param x_data: 数据集合
    :param y_data: 数据类别
    :return: 切分点
    '''
    w = np.size(x_data,axis=1)
    count = []
    count_label = {}
    for i in range(w):
        if dis_or_con[i] == 0:
            a = Gini_D_A(x_data,y_data,i)
        else:
            a = Gini_continuous(x_data,y_data,i)
        count.append(a[1])
        count_label[i] = a
    id = count.index(min(count))
    return id,count_label[id][0]

决策树的生成

  决策树的生成大致与ID3算法类似

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def create_tree(x_data,y_data,dis_or_con_data,feature_list_data):

    feature_list = feature_list_data[:]
    dis_or_con = dis_or_con_data[:]
    if dis_or_con == []:
        return most_y_data(y_data)
    if is_all_same(y_data):
        return y_data[0]
    w,f = choose_feature(x_data,y_data,dis_or_con)
    count_x, count_y = feature_split(x_data,y_data,w,f,dis_or_con[w])
    node_name = feature_list[w]
    tree = {(node_name,f):{}}
    del feature_list[w]
    del dis_or_con[w]
    for i in count_x.keys():
        fealist = feature_list[:]
        dis_con = dis_or_con[:]
        count_x_del = del_feature(count_x[i], w)
        tree[(node_name,f)][i] = create_tree(count_x_del, count_y[i], dis_con,fealist)
    return tree

剪枝

  本文暂未实现剪枝算法，有待后续补充


    本文作者：光阴的故事

    本文链接： 决策树.html/

    版权声明： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处！
坚持原创技术分享，您的支持将鼓励我继续创作！