维吉尼亚加解密及唯密文破解

摘要古典密码体制主要通过字符间的置换和代换来实现，常见的置换密码包括列置换密码和周期置换密码，而常见的代换密码包括单表代换密码和多表代换密码，本文所讨论的维吉尼亚算法是属于多表代换密码的一种。多表代换密码是以一系列代换表依次对明文消息的字母序列进行代换的加密方法，即明文消息中出现的同一个字母，在加密时不是完全被同一固定的字母代换，而是根据其出现的位置次序用不同的字母代换。如果代换表序列是非周期的无限序列，则相应的密码称为非周期多表代换密码，这类密码对每个明文都采用了不同的代换表进行加密，故称为一次一密密码，它是理论上不可破译的密码体制。但实际应用中经常采用的是周期多表代换密码，它通常使用有限个代换表，代换表被重复使用以完成消息的加密。作为多表代换密码的典型代表，维吉尼亚密码算法蕴含着丰富的古典密码设计思想，本文将深入探讨维吉尼亚算法的加解密过程实现，以及利用统计分析的方法进行唯密文攻击。

avatar

文章概览

维吉尼亚算法简介
加密算法实现
- 编码方式
- 对明文进行处理
- 加密过程
解密算法实现
唯密文攻击
- 确定密钥长度
- 确定密钥
- 恢复明文

维吉尼亚算法简介

加密算法实现

实现加密算法的大致流程是：首先我们需要确定编码方式，本文采用的编码方式是[a-z]对应[0-25]；接着进行加密算法前需要对明文字符串进行处理，删除非字母字符，将大写字符统一转换为小写字母；最后选定密钥对密文中的逐个字符进行加密（即代换操作），生成最后的密文。

编码方式

本文的字母编码方式由列表s确定，s中每个元素的索引即对应该元素的数字编码。

1	s = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']

对明文进行处理

对明文进行处理的目的是去除明文中非字母的字符，并将大写字母统一转换为小写字母。转换大小写我们可以使用python字符串内置的lower()函数，稍微有点棘手的是前者，因为在这里需要考虑到一些效率的问题还有如何对后续操作进行优化的问题，比如说:

读取文件中的明文时我们可以采用read()，readline()，readlines()这三个函数，那我们到底采用哪一个呢？（这三个函数的对比可以参考这篇博客)
采用不同读取明文的函数，导致读取结果也不尽相同，有列表形式也有字符串形式，到底哪种形式对后续的操作更有好处
去掉读取后的明文中的非字母字符应采用何种方式？（逐个字符判断或者正则表达式）

本文根据文本的实际情况，采用的处理方式如下所示

def pretreatment():
    """
    pretreatment函数的主要作用是对明文进行预处理，去除非字母字符和转换大小写
    :return: 经过预处理的明文字符串
    """
    with open("plain.txt","r") as f:
        wen = f.read()
    pattern = re.compile('[\n]|\d|\W')
    plain_1 = re.sub(pattern,'',wen).lower()
    return plain_1

加密过程

维吉尼亚算法的加密过程比较简单，基本思想是利用密钥循环对明文字符进行代换操作，进行代换前将相应的明文字符和密钥字符转化为对应的数字编码，然后相加对26取余即得到对应的密文字符。

def encrypt(key):
    """
    encrypt函数的主要作用是进行加密
    :param key: 密钥
    :return: 密文字符串
    """
    wen = pretreatment()
    num_key = key_to_num(key)
    ciphertext = ''
    k = 0
    for w in wen:
        if k == len(num_key):
            k = 0
        cipher = change(w,num_key[k])
        cipher = num_to_char(cipher)
        ciphertext = ciphertext + cipher
        k += 1
    wirte_txt(ciphertext,'crypt.txt')
    return ciphertext

解密算法实现

解密算法是加密算法的逆过程，进行的代换操作是将密文字符的数字编码减去密钥字符的数字编码，如果相减的结果小于0，则令结果加上26，在转换为对应编码的字符。

def de_change(ch,num):
    """
    de_change函数的作用是根据密文字符和密钥还原明文字符
    :param ch: 密文字符
    :param num: 密钥编码
    :return: 明文字符
    """
    ch_num = char_to_num(ch)
    result = ch_num - num
    if result < 0:
        result = 26 + result
    return result

def decrypt(key):
    """
    decryption函数的主要作用是将密文解密成明文
    :param key: 密钥
    :return: 明文
    """
    with open('crypt.txt','r') as f:
        ciphertext = f.read()
    num_key = key_to_num(key)
    wen = ''
    k = 0
    for c in ciphertext:
        if k == len(num_key):
            k = 0
        w = de_change(c,num_key[k])
        w = num_to_char(w)
        wen = wen + w
        k += 1
    wirte_txt(wen,'result.txt')
    return wen

唯密文攻击

某种语言中各个字符出现的频率不一样而表现出一定的统计规律，而这种统计规律可能在密文中重现，所以我们可以通过统计分析的手段进行一些推测和验证过程来实现对密文的分析。在英文字母中各个字母出现的频率如下所示，

#编码规则
s = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
#字母出现频率
frequency = [0.082,0.015,0.028,0.043,0.127,0.022,0.02,0.061,0.07,0.002,0.008,0.04,0.024,0.06,0.075,0.019,0.001,0.06,0.063,0.091,0.028,0.01,0.023,0.001,0.02,0.001]

对于维吉尼亚密码体制来说，我们可以通过统计分析的方法对其密文进行分析，从而获取明文信息。基于维吉尼亚密码体制的唯密文攻击的破解主要包含三个步骤：

确定密钥长度，常用的方法包括卡西斯基测试法和重合指数法，本文将采用后者进行分析
确定密钥，常用的方法是拟重合指数法
根据密文和密钥恢复明文

确定密钥长度

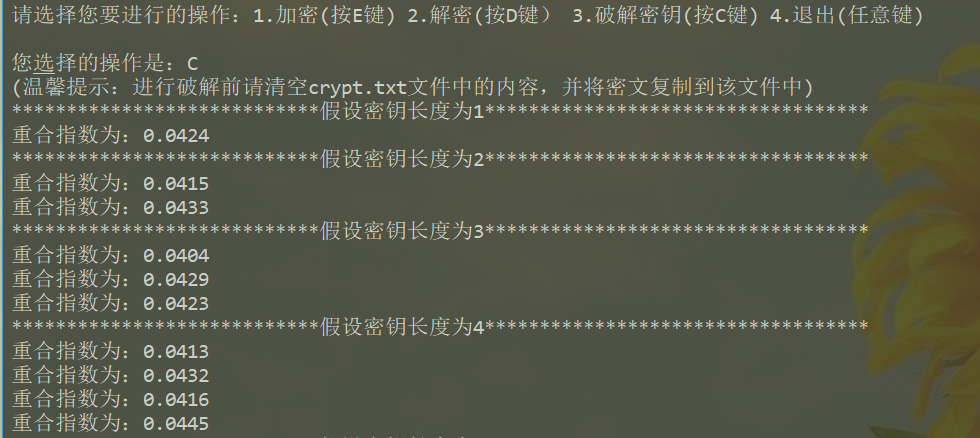
本文采用重合指数法猜解密钥长度，关于重合指数法的具体解释可以参照《现代密码学教程》或者维基百科，本文主要讲解猜解密钥长度的实现过程。

def guess_len_key(crypt):
    """
    guess_len_key函数的主要作用是通过密文猜解密钥长度
    :param crypt: 密文
    :return: 密钥长度以及划为的子串
    """
    l = 1
    d = {}
    while True:
        print("****************************假设密钥长度        为%s***********************************" % l)
        sum_index = 0.0
        for i in range(len(crypt)):
            n = i % l
            if n not in d:
                d[n] = ''
            d[n] += crypt[i]
        sum_index = sum(coincidence_index(d[j]) for j in range(l)) / l
        if sum_index >= 0.06 and sum_index <= 0.07:
            break
        else:
            l += 1
            d = {}
    return l,d

该算法的主要思想是将密文划分为l个子串，子串存放在字典d中。分别计算l个子串的重合指数，然后计算l个重合指数的平均数，如果该平均数位于[0.06,0.07]这个区间内，则说明密钥长度为l，返回密钥长度以及划分的l个子串；如果得到的平均数不在[0.06,0.07]这个区间内，则l自增，d初始化，进行下一轮猜解。

确定密钥

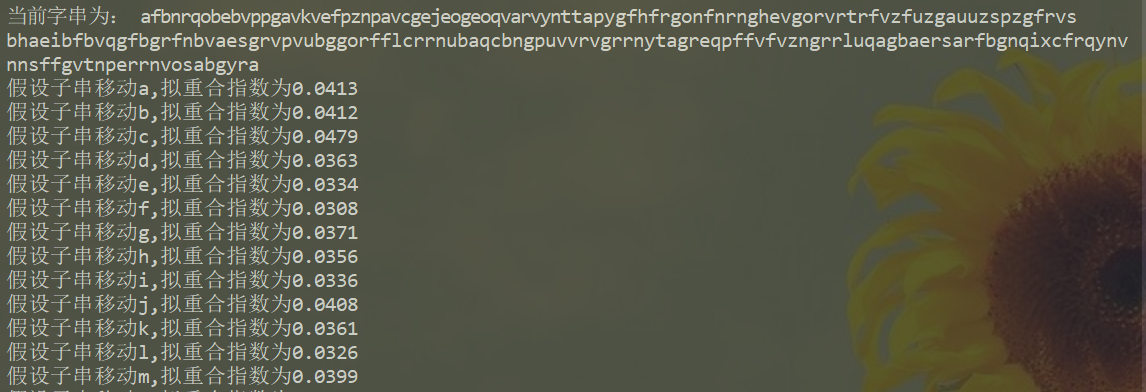
确定密钥长度大致过程是：利用之前得到的l个子串，对每个子串都进行移位操作。假设现在对第i个子串进行移位操作（子串的每个字符移动相同的位数，最坏情况下对同一个子串需要进行26次移位操作），移动的位数为k,（k在[0-25]区间内，也就对应了[a-z]）。每进行一次移位操作，就对该子串计算一次拟重合指数，如果该拟重合指数位于[0.06,0.07]这个区间内，则说明此时移动的位数对应的s列表中的字符即为该子串的密钥；否则，继续进行下一次移位操作。

def crack_key():
    """
    cracker函数的主要作用是破解密钥
    :return: 返回密钥
    """
    with open("crypt.txt","r") as f:
        crypt = f.read()
    len_key,d = guess_len_key(crypt)
    key = ''
    print("\n-------------------------------------")

    print("|       经计算可知，密钥长度为%s         |" % len_key)
    print("-------------------------------------\n")
    for i in range(len_key):
        substring = d[i]
        print("当前字串为：",d[i])
        for n in range(26):
            dex = quasi_index(substring, n)
            print("假设子串移动{},拟重合指数为{:.4f}".format(s[n],dex))
            if dex >= 0.06 and dex <= 0.07:
                key += s[n]
                break
    print("******************************破解的最终密钥为%s*********************************" % key)