摘要:近些年来,深度学习技术在海量数据以及强大计算能力的驱动下取得了长足的发展,特别是在语音识别、计算机视觉、自然语言处理等领域,深度学习以其强大的网络表达能力刷新了一项又一项记录,各种各样基于深度学习的产品和服务也逐渐在产业界落地应用。正因为深度学习技术蕴含着巨大的商业价值,其背后潜在的安全问题更值得我们去深究。最近的研究表明,深度学习面临安全和隐私等多方面的威胁。该系列主要讨论深度学习领域最为热门的安全问题–对抗样本。本文讨论的FGSM和DeepFool是较为的早期对抗样本的生成算法,除此之外还会对DeepFool衍生出的Universal Perturbation进行解读。

文章概览
- FGSM
- 算法概述
- 代码实现
- DeepFool
- 算法概述
- 代码实现
- Universal Perturbation
FGSM
算法概述
在机器学习领域,对抗样本的问题始终存在。特别是在入侵检测、垃圾邮件识别等传统的安全应用场景,对抗样本的生成和识别一直是攻击者和防御者博弈的战场。2013年,Szegedy等人首次提出针对深度学习场景下的对抗样本生成算法–BFGS,作者认为,深度神经网络所具有的强大的非线性表达能力和模型的过拟合是可能产生对抗性样本原因之一。2014年,Goodfellow等人(包括Szegedy)对该问题进行了更深层次的研究,它们认为高维空间下深度神经网络的线性线性行为是导致该问题的根本原因。并根据该解释,设计出一种快速有效的生成对抗性样例的算法–FGSM。以下是对论文的解读。
对于线性模型$f(x)=w^Tx+b$来说,如果我们对输入$ x $添加一些扰动,使得$ \tilde{x}=x+\eta $。为了确保添加的扰动是极小的或者说是无法感知的,我们要求$ \left|\eta\right|_\infty<\epsilon $。所以我们可以得到加噪后的模型输出为
$$
f(\tilde{x})=w^Tx+w^T\eta+b
$$
为了尽可能增大添加的噪声对输出结果的影响,令$\eta=\epsilon sign(w)$(sign()函数的定义)。如果$w$是一个$n$维的向量,每一维的均值为$m$,则$w^T\eta=\epsilon nm$。虽然$\epsilon$的值很小,但是当$w$的维度$n$很大时,$\epsilon nm$将是一个很大的值,这将会给模型的预测带来很大的影响。因此,高维特征和线性行为可以成为对抗性样本存在的一种解释。
上面的解释是基于线性模型而言的,而深度神经网络作为一种高度非线性模型,为什么会存在对抗性样例呢?深度神经网络的非线性单元赋予了其强大的表达能力,但是非线性单元的存在会降低学习的效率。为了提高学习效率,需要对非线性单元进行改进,通常的做法是通过降低其非线性来实现。从早期的sigmoid到tanh再到ReLU,我们会发现这些非线性单元的线性行为在不断增强,这也导致了深度神经网络中的线性能力的增强,这在一定程度上解释了深度神经网络中对抗性样例存在的原因。
根据这种解释,作者提出了生成对抗性样例的算法FGSM。我们将深度神经网络模型看作是一个线性模型,即类似于$f(x)=w^Tx+b$。在线性模型中,$w$为$f(x)$关于$x$的导数,而在深度神经网络模型中我们可以将$w$视为代价函数关于输入$x$的导数,即
$$
w=\nabla_{x}J(\theta,x,y)
$$
$$
\eta=\epsilon sign(\nabla_{x}J(\theta,x,y))
$$
在文章的后半部分主要介绍了针对对抗性样本的防御机制,即通过对抗性训练来提高模型的鲁棒性,这些内容会在之后的工作中讨论。
代码实现
为了更好的理解算法的实现过程,以下给出本文相关的代码段。这些代码段给出的定义,对于后面的DeepFool和Universal Perturbation算法的解读依赖有效。所有的代码基于python实现,使用的深度学习框架为pytorch,更加完整的算法实现参见我的github.
网络模型
1
2
3
4
5
6
7
8
9
10
11class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(28*28, 300)
self.fc2 = nn.Linear(300, 100)
self.fc3 = nn.Linear(100, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x数据集(这里只给出测试集的数据定义)
1
2
3
4
5# 定义数据转换格式
mnist_transform = transforms.Compose([transforms.ToTensor(), transforms.Lambda(lambda x : x.resize_(28*28))])
# 导入数据,定义数据接口
testdata = torchvision.datasets.MNIST(root="./mnist", train=False, download=True, transform=mnist_transform)
testloader = torch.utils.data.DataLoader(testdata, batch_size=256, shuffle=True, num_workers=0)代价函数
1
loss_function = nn.CrossEntropyLoss()
FGSM算法的实现较为简单,其核心在于利用代价函数求解已知样本的梯度值。我们假设模型已经训练完成,首先我们加载已训练完成的深度网络模型
1 | net = torch.load('mnist_net_all.pkl') # 加载模型 |
然后我们选择一个测试样本,针对该测试样本生成其对应的对抗性样例。其原始图片格式如图所示。
1 | index = 100 # 选择测试样本 |
接着将测试样本作为网络模型的输入,通过前向传播的过程计算其损失,然后利用其损失进行反向传播(即求导)。
1 | outputs = net(image) # 前向传播 |
在深度学习框架中,反向传播的过程对用户来说是透明的。计算结束后,其梯度值存储在image.data.grad中,添加扰动的过程如下
1 | # FGSM添加扰动 |
添加扰动后,得到对抗性样本如下所示
实验过程中我们发现,深度网络模型对于原始的图片能够正确的分类,而对于扰动之后的的样本不能正确分类(分类结果为2)。
DeepFool
算法概述
FGSM算法能够快速简单的生成对抗性样例,但是它没有对原始样本扰动的范围进行界定(扰动程度$\epsilon$是人为指定的),我们希望通过最小程度的扰动来获得良好性能的对抗性样例。2016年,Seyed等人提出的DeepFool算法很好的解决了这一问题。文章的核心思想是希望找到一种对抗性扰动的方法来作为对不同分类器对对抗性扰动鲁棒性评估的标准。简单来说就是,现在我需要两个相同任务的分类器A、B针对同一个样本生成各自的对抗性样例。对于分类器A而言,其生成对抗性样例所需要添加的最小扰动为$a$;对于分类器B而言,其生成对抗性样例所需要添加的最小扰动为$b$;通过对$a$、$b$的大小进行比较,我们就可以对这两个分类器对对抗性样例的鲁棒性进行评估。由于FGSM产生扰动是人为界定的,所以它不能作为评估的依据。DeepFool可以生成十分接近最小扰动的对抗性样例,因此它可以作为衡量分类器鲁棒性的标准。
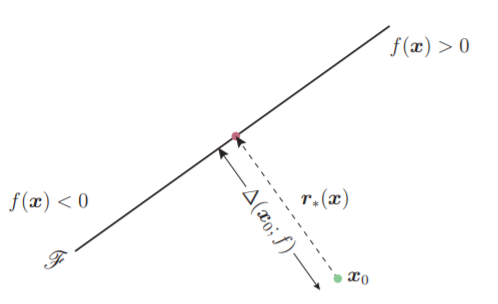
DeepFool源于对分类问题的思考。对于如图所示的线性二分类问题,令$f(x)=w^Tx+b$,其中$\mathscr{F}={x : f(x)=0}$。此时$x_0$位于直线的下方,即$f(x_0)>0$。现在我们希望对$x_0$添加扰动$r$,使得分类器$f(x_0+r)<0$。那么如何添加扰动才能使得扰动的程度最小呢?这个问题可以转化为求点到直线之间的距离,我们通过$x_0$做直线$\mathscr{F}$的垂线,与$\mathscr{F}$相交于$p$(投影点),则$p$与$x_0$之间的距离即为$x_0$到分类边界$\mathscr{F}$的最短距离。所以当我们沿着分类边界法线方向对$x_0$进行扰动,可以保证扰动的程度最小
$$
r(x_0):={\arg\min_k}{|{r}|_{2}}=-{\frac{f(x_0)}{|{w}|_{2}^{2}}{w}}
$$
添加扰动之后将$x_0$映射到分类边界的投影点$p$,即$p=x_0+r(x_0)$。
同样,对于非线性的二分类问题(分类边界为曲线或者曲面),我们也需要计算从目标样本点到分类边界的最短距离。这个计算过程较为复杂,一般采用垂直逼近法来逐步的逼近$x_0$在分类边界上的投影点,所以在论文中算法1会有一个迭代过程。值得注意的是,我们得到最终的$\sum_i{r_i}$表示的是从$x_0$到分类边界投影点的距离向量,满足$f(x_0+\sum_i{r_i})=0$。如果要使分类结果改变,需要再添加一些极小的扰动,如$f(x_0+(1+\eta)\sum_i{r_i})<0$(文中$\eta$取0.02)。
对于多分类任务,思路也大致相同。在线性多分类任务中,需要注意的大致有两点:首先,对于多分类任务的分类边界要重新进行定义。我们令$f(x)$为分类器,$\hat{k}(x)=\mathop{\arg\max}_{k}{f_k(x)}$表示其对应的分类结果(一共有$k$个类别)。分类边界定义为
$$
\mathscr{F}_k={x : f_k(x)-f_{\hat{k}(x_0)}(x)=0}
$$
其次,由于分类边界有多个,我们需要以此求出$x_0$到每个分类边界的距离(类似于进行多次二分类的计算过程),然后进行比较,选择其中最短距离向量作为最终的扰动。
$$
\hat{l}(x_0)=\mathop{\arg\min_{k \neq \hat{k}_{x_0} }}{\frac{|f_k(x_0)-f_{\hat{k}(x_0)}(x_0)|}{|{w_k -w_{\hat{k}_{x_0}}}|_2}}
$$
之后通过计算$\boldsymbol{r}(x_0)$得到$x_0$在分类边界上的投影。
在非线性多分类任务中,与线性多分类的区别在于其分类边界是不确定的,所以我们需要采用类似于非线性二分类任务中的方法来逼近分类边界。获得分类边界之后的计算与线性多分类的过程类似。此后,重复该过程多次,即可获得最终$x_0$在分类边界的投影。
代码实现
以下讨论多分类情况下DeepFool算法的代码实现,模型结构以及数据集等与上述一致,不再重复。首先,我们选择一个测试样本,生成该样本的对抗性样例。
1 | net = torch.load('mnist_net_all.pkl') # 加载模型 |
接下来,通过前向传播的过程,我们获得该样本对每一类别可能的取值情况,并将其从大到小排列起来,列表$I$对应其索引值,$label$即$\hat{k}_{x_0}$。
1 | f_image = net.forward(image).data.numpy().flatten() |
然后,我们定义一些需要用到的变量
1 | input_shape = image.data.numpy().shape # 获取原始样本的维度 |
下面是算法实现的核心部分,参考论文中的伪代码,其中orig_grad表示$\nabla f_{\hat{k}_{x_0}}(x_i)$,cur_grad表示$\nabla f_k(x_i)$,fs[0][I[k]]表示$f_k(x_i)$,fs[0][I[0]]表示$f_{\hat{k}_{x_0}}(x_i)$。通过内部的for循环可以获得x到各分类边界的距离;在外部的while循环中,我们利用内部循环获得的所有边界距离中的最小值对x进行更新。重复这一过程,直到$x$的分类标签发生变化。
1 | while k_i == label and loop_i < max_iter: |
对原始图片,添加扰动获得如下图片(分类器将其错误分类为2,有些奇怪的地方在于其扰动的程度要大FGSM,算法应该没有问题,一直没找到原因)。
Universal Perturbation
前面介绍的FGSM和DeepFool算法,它们都是针对单个样本生成其对抗性样例,也就是说每个对抗性样例的扰动程度都不同。那么是否能找到一种通用性的扰动边界,能够为不同的样本生成对抗性样例。在DeepFool工作的基础上,Seyed 等人提出了Universal Perturbation,该算法为寻找通用性扰动边界提供了可能。以下简单介绍一下论文的核心思想:
- 从数据集中随机选取部分测试样本作为生成通用性扰动边界的范例,通过这些测试样本生成的通用性扰动适用于整个数据集。
- 算法的计算过程:输入第一个样本后,通过DeepFool算法找到该样本的最小扰动距离向量,将其累积到通用扰动向量$v$中(对$v$的扰动程度会有限制和调整,${|v|_p<\xi}$);当输入第二个样本之后,对其添加$v$的扰动之后,然后再通过DeepFool计算扰动后的样本的最小扰动距离向量,将其累积到通用扰动向量$v$中(对$v$的扰动程度会有限制和调整,${|v|_p<\xi}$)。重复这一过程,直到最后一个测试样本。然后,我们使用通用扰动向量$v$,对原始的测试样本进行扰动,测试其生成对抗性样例的成功率。如果小于预先设置的阈值$1-\delta$,则跳出循环返回结果。否则,重复上述过程。
- 通用性扰动对不同的网络模型依然有效。也就是说,利用网络模型A生成的通用性扰动,同样适用于生成网络模型B的对抗性样例(A、B是不同类型的网络架构)。
本文作者:光阴的故事
本文链接: 对抗样本生成系列:FGSM和Deepfool.html/
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处!