深度神经网络实现解析

摘要：最近一段时间在回顾深度学习的一些基本知识，感觉对有些内容的理解比较模糊，于是萌生了手动来实现的想法。其实类似的工作之前也做过，写过决策树、支持向量机、神经网络等，不过当时是用numpy写的。因为现在一直在使用pytorch，pytorch中的tensor与numpy中的array很相似，所以这次的代码主要使用tensor来实现。目前实现的代码包括逻辑回归、softmax回归、深度神经网络和卷积神经网络，所有的代码都可以在我的github中找到。这篇博客主要来记录在实现深度神经网络过程中的一些思路，以及遇到的问题。

文章概览

深度神经网络简介
深度神经网络框架实现
- 整体思路
- 前向计算
- 反向传播
交叉熵损失函数与softmax激活函数

深度神经网络简介

网上对深度神经网络（DNN）介绍的文章很多，这里不再赘述。推荐一些资料：刘建平博客、复旦大学邱锡鹏教授神经网络与深度学习。

深度神经网络框架实现

整体思路

在使用pytorch、tensorflow等框架来构建一个深度神经网络模型的时候，通常全连接层和激活函数层分开进行定义的。通过这种模块化的方式有利于自由的设计模型，在本文的代码中依然沿用这种方式。首先，我们需要定义一个父类，所有的全连接层以及激活函数层均继承自该父类。神经网络中的每一层都实现统一的方法接口，包括前向计算和反向传播，这样我们可以实现数据在神经网络模型中流动时的一致性。每一层可以根据自身的处理逻辑来重写继承自父类的方法，并且可以根据需要来增加成员方法和变量，例如全连层需要定义权重和偏值，而激活函数层则不需要。除此之外，在反向传播过程中，我们使用SGD算法来对参数进行更新。由于我们采用模块化的方式构建模型，所以神经网络的不同层之间相对独立，对于不同的层我们可以设置不同的学习率。

# 全连接层以及激活函数层均继承自该父类
class Layer:
    def __init__(self):
        pass
    def forward(self, input):
        return input
    def backward(self, input, grad):
        pass

前向计算

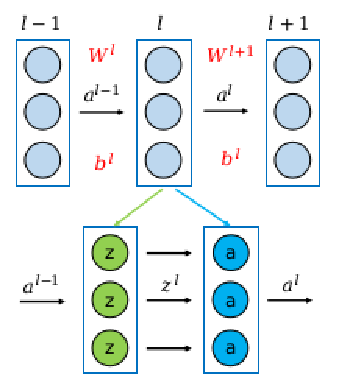
前向计算的过程较为简单，网络中每一层所需要做的就是将该层输入传入self.forward函数，根据内部逻辑返回输出，该输出又将作为下一层的输入。对于全连接层，假设输入为$a^{l-1}$，计算$z^l=(W^l)^T*a^{l-1}+b^l$，再将$z^l$传递到下一层；对于激活函数层，假设输入为$z^l$，计算$a^l=\sigma(z^l)$，再将$a^l$传递到下一层。需要注意的是，我们需要记录下神经网络中的每一层的输入值$a^i$，在反向传播更新权重时会用到。

def forward(network, x):
    # 前向传播
    activations = []
    input = x
    for layer in network:
        activations.append(layer.forward(input))
        input = activations[-1]      
    return activations

反向传播

对于反向传播而言，每一层的处理逻辑大致相同，即将该层输出值的误差项作为self.backward函数的输入，经过计算得到该层输入值的误差项，继续反向传播。需要注意的是，由于全连接层含有偏置和权重，在反向传播时除了需要计算误差项之外，还需要更新偏置和权重。反向传播算法的推导过程可以参考这篇博客，这里给出以下结论：
$$
\delta^{l}=(W^{l+1})^{T} \delta^{l+1} \odot \sigma^{\prime}(z^{l})
$$

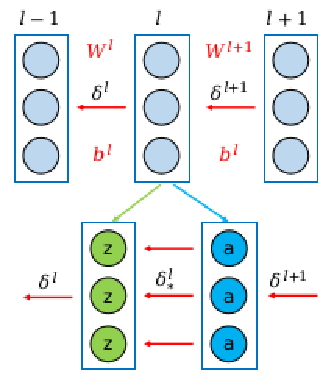
在很多介绍神经网络的书中，通常将一个全连接层和一个激活函数构成的整体当作神经网络的一层。但是，在我们代码中是将二者分开的，所以我们需要对上式进行改写。上式中$\delta^{l+1}$表示神经网络第$l+1$层输入值的误差项，即$a^l$的误差项；$\delta^{l}$表示神经网络第$l$层输入值的误差项，即$a^{l-1}$的误差项。由于我们将第$l$层拆分为两层，所以我们先要计算激活函数层输入值的误差项（记做$\delta^l_*$)，再计算全连接层输入值的误差项$\delta^{l}$。所以我们得到下面的公式：
$$
\delta^{l}_{*}= \delta^{l+1} \odot \sigma^{\prime}(z^{l})
$$

$$
\delta^{l}=(W^{l+1})^{T} \delta^{l}_{*}
$$

通过这种转换，实现了不同层之间数据流动的一致性，即反向传播时，不论是全连接层还是激活函数层都是接受其输出值的误差项，返回其输入值的误差项。除此之外，由于在全连接层需要对权重和偏置进行更新，需要$a^{l-1}$作为参数，所以在self.backward的参数列表中加入该项。虽然激活函数层不需要更新参数，但是为了统一写法，也会加入这一参数。以下给出全连接层的backward函数。
$$
\frac{\partial J(W, b, x, y)}{\partial W^{l}}=\delta^{l}\left(a^{l-1}\right)^{T}
$$

$$
\frac{\partial J(W, b, x, y)}{\partial b^{l}}=\delta^{l}
$$

def backward(self, input, grad):
    grad_input = torch.mm(grad, self.w.T)
    dw = torch.mm(input.T, grad) / input.shape[0]
    db = torch.sum(grad, axis=0) / input.shape[0]
    self.w -= self.learning_rate*dw
    self.b -= self.learning_rate*db
    return grad_input

交叉熵损失函数与softmax激活函数

使用神经网络处理多分类问题的时候，我们往往会使用交叉熵损失函数与softmax激活函数组合的形式，即将神经网络最后一层的激活函数设置为softmax，模型整体的损失采用交叉熵来进行计算。在这之前，我对二者的理解停留在比较浅显的层面：softmax函数将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解；交叉熵损失函数可以衡量两个概率分布之间的相似性，即softmax的输出和训练数据标签onehot编码之间的相似性。除此之外，交叉熵损失函数与softmax激活函数组合更深层次的原因体现在计算层面，它能够简化反向传播的计算过程。以下，我们对该问题进行分析。

假设我们现在要计算softmax激活函数层输入值的误差项$\delta^{l}_{*}$，根据我们上面的得到的公式，我们需要分别计算$\delta^{l+1}$和$\sigma^{\prime}(z^{l})$。因为softmax是神经网络的最后一层，所以这里的$\delta^{l+1}$等于交叉熵损失函数对softmax输出值的导数$\frac{\partial J}{\partial a^{l}}$。而$\sigma^{\prime}(z^{l})$则表示softmax函数对其输入进行求导$\frac{\partial a^{l}}{\partial z^{l}}$。

按照常规思路，我们需要单独计算这两个过程。但是对于交叉熵损失函数与softmax激活函数组合情况而言，可以将这两个过程进行合并，可以直接推导出$\frac{\partial J}{\partial z^{l}}$的值。具体的推导过程，可以参考这篇博客，这篇博客是我目前看过最简单易懂的，这里给出结论：
$$
\delta^{l}_{*}=\frac{\partial J}{\partial z^{l}}=a^l-y
$$
可以看出这个结论十分简洁优美，所以当我们使用交叉熵损失函数与softmax激活函数组合形式的时候，softmax层的backwrad函数只需要将$a^l-y$返回即可，无需进行任何操作。

# softmax激活函数作为神经网络最后一层
class Softmax(Layer):
    def __init__(self):
        pass
    
    def forward(self,input):
        exp = torch.exp(input)
        exp_sum = torch.sum(exp, axis=1, keepdims=True)
        return exp / exp_sum
    
    def backward(self,input,grad):
        return grad

值得注意的一点是，在使用pytorch框架构建神经网络来实现多分类任务时，如果我们的代价函数使用torch.nn.CrossEntropyLoss()（交叉熵），网络的最后一层无需再定义softmax层，并且数据标签也不需要修改为onehot编码，这些逻辑在其内部应该都会实现，具体操作请参考我的代码。

本文作者：

本文链接：

深度神经网络实现解析.html/

CC BY-NC-SA 3.0 CN