卷积神经网络实现解析

发表于 | 分类于 |
字数统计: 3,568 | 阅读时长 ≈ 14

摘要：卷积神经网络是受生物学中感受野机制的启发而提出的，是一种具有局部连接、权重共享等特性的深层前馈神经网络，其主要应用于图像和视频分析等领域。2012年，卷积神经网络在ImageNet大规模视觉识别挑战竞赛中大放异彩，一定程度上引领了深度学习袭卷全球的潮流。这篇文章聚焦于卷积神经网络的实现细节，本文我们将使用pytorch中的tensor实现一个简单的卷积神经网络框架（很多文章采用的是numpy实现），并在FashionMnist数据集中进行测试。文中给出实现过程中的部分代码，完整的代码可以在我的github中找到。

文章概览

  • 卷积神经网络简介
  • 卷积层的实现细节
    • 前向计算
    • 反向传播
  • 池化层的实现细节
    • 前向计算
    • 反向传播
  • 测试结果

卷积神经网络简介

  在前面的文章中我们讲到了全连接前馈网络，并且在FashionMnist数据集上对我们构建的网络框架进行了测试。简单回顾一下当时的数据处理过程，FashionMnist数据集中的图片通道数为1、图片尺寸为28×28，原始数据集表示为$ X=(N, 1, 28 ,28) $。在训练之前，我们需要将训练数据转化为 $ X=(N, 1*28*28) $，相当于将数据集中每一张图片的像素点展开成向量的形式。显而易见，将图片展开为向量会丢失空间信息，这会对模型的泛化性能产生很大的影响。除此之外，利用全连接前馈网络处理图像数据往往会需要很多的参数。举例来说，假设现在数据集中的图片为100×100的彩色图片，此时每张图片中包含的像素点为$ 3*100*100 $，即$ X=(N, 3*100*100) $。如果第一个隐藏层有1000个神经元，那么仅该层包含的参数个数为$ 30000*1000 + 1000 $。过多的参数会给模型的训练过程造成很大的负担，同时也会导致过拟合等问题。综上所述，一般情况下我们不采用全连接前馈网络来处理图像数据。

  卷积神经网络最早主要是用来处理图像信息，是受生物学中感受野机制的启发而提出的（感受野是指卷积神经网络每一层输出的特征图上的像素点在输入图片上映射的区域大小。通俗点的解释是，特征图上的一个点对应输入图上的区域）。1998年，LeCun提出了经典的卷积网络模型LeNet-5，第一次较为完整的阐述了卷积神经网络的框架和结构。卷积神经网络由输入层、卷积层、激活层、池化层、全连接层及输出层构成。卷积层和池化层一般会取若干个，采用卷积层和池化层交替设置，即一个卷积层连接一个池化层，池化层后再连接一个卷积层，依此类推。与全连接前馈网络相比，卷积神经网络在结构上具有局部连接、 权重共享、降采样等特点，并且在训练过程中会完整保留数据的空间信息。这些特性使得卷积神经网络图像处理领域表现更加出色，并且使用的参数更少。

CNN层次结构 作用
输入层 卷积网络的原始输入，可以是原始或预处理后的像素矩阵
卷积层 参数共享、局部连接，利用平移不变性从全局特征图提取局部特征
激活层 将卷积层的输出结果进行非线性映射
池化层 进一步筛选特征，可以有效减少后续网络层次所需的参数量
全连接层 将多维特征展平为2维特征，通常低维度特征对应任务的学习目标（类别或回归值）

以下主要介绍卷积神经网络中卷积层和池化层的实现细节，激活层和全连接层的实现与全连接前馈网络基本一致，这里不再赘述，具体代码参考我的github（需要注意的是，本文实现代码中，默认输入图片高度和宽度相同）。

卷积层实现细节

  开始介绍之前，简要说明参数设置情况。输入数据尺寸为$s=5$，通道数为$in_channel=3$，即$ input=(n, 3, 5, 5)$；单个卷积核尺寸为$k=2$，卷积层输出通道数为$out_channel=10$，即$kernel=(10, 3, 2, 2)$；假设卷积步幅$stride=1$，$pad=0$，根据特征图大小计算公式
$$
p=\frac{s-k+2*pad}{stride}+1
$$
则卷积层输出为$output=(N, 10, 4, 4)$。

前向计算

  在卷积神经网络中所使用的卷积，一般是指互相关操作，其本质上就是利用卷积核在输入数据上进行滑动，并在滑动窗口内计算点积，计算过程如如下图所示。

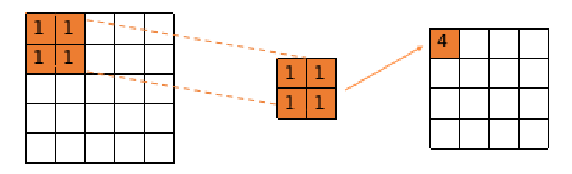
  如果将该操作拓展到多通道的情况，我们需要将每一个通道数据与其对应的卷积核分别进行互相关操作，每个通道都会得到一个输出，然后将所有输出相同位置相加，得到最终的特征图，计算过程如下所示。

  这一过程最简单的思路是通过多重循环来实现，但是这种实现方式会极大降低训练过程的效率。im2col算法通过将这一过程转化为矩阵乘法的形式可以极大程度提升计算效率，该算法的主要思想如下图所示。

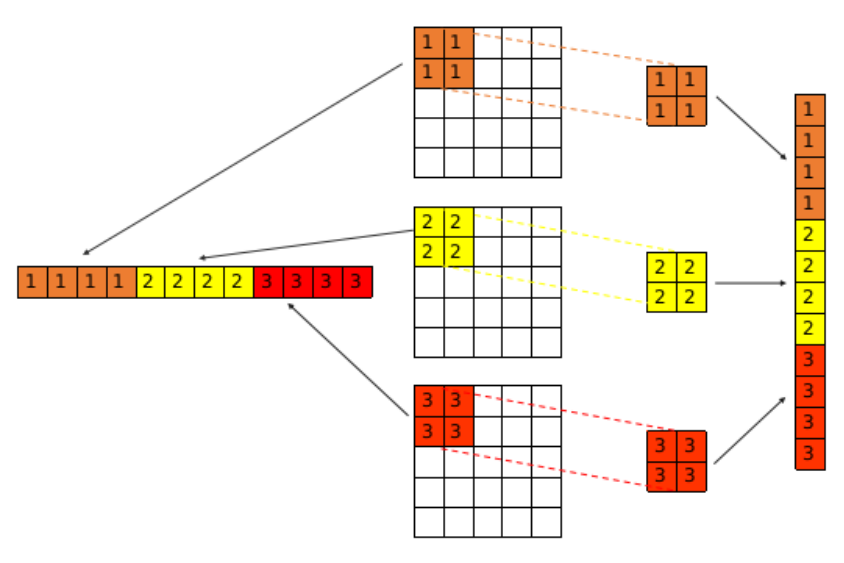
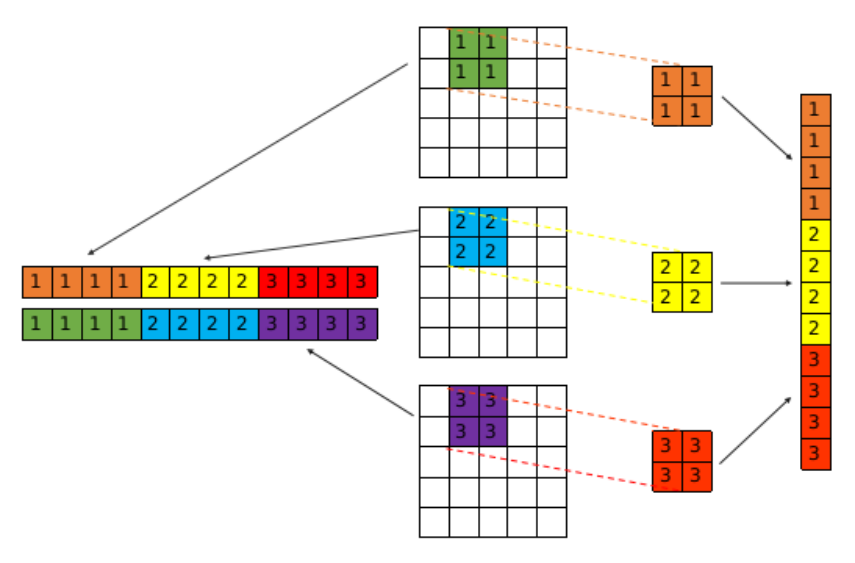
  im2col的核心思想是将每个卷积核在其对应通道上滑动过程中滑动窗口位置上的数据重新排列，组合成一维行向量的形式，而卷积核自身则排列成列向量的形式。卷积层输出的特征图中的每一个值都能表示成上述行向量和列向量相乘的形式。如果含有多层卷积核，则如下图方式排列。

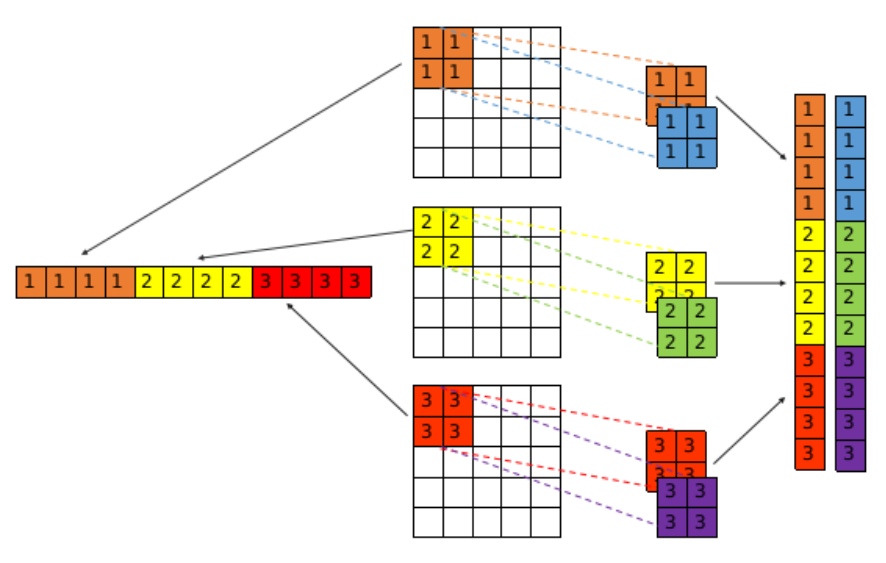
通过这种方式，我们的输入数据可以成$input=(n*p*p, k*k*in_channel)$，卷积核可表示为$kernel=(k*k*in_channel, out_channel)$。该过程的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def im2col(self, input):
    n, in_channel, s, _ = input.shape
    p = (s - self.k_size) // self.stride + 1
    im = torch.zeros((n*p*p, k*k*in_channel))
    for i in range(p):
        i_start = i*self.stride
        i_end = i_start + self.k_size
        for j in range(p):
            j_start = j*self.stride
            j_end = j_start + self.k_size
            im[i*p+j::p*p, :] = input[:,:,i_start:i_end,j_start:j_end].reshape(n, -1)

    w = self.w.reshape(self.k_size**2*c, self.out_channel)
    output = torch.matmul(im, w) + self.b
    return output.reshape(n, self.out_channel, p, p)

反向传播

  在反向传播过程中，卷积层主要做两件事：（1）利用卷积操作的输出层的误差项$\delta^l$来求卷积操作输入层的误差项$\delta^{l-1}$，并将结果继续反向传播；（2）求解卷积核的梯度，并对其进行更新（反向传播的过程可以参考这篇博客）。首先我们来求解输入层的误差项$\delta^{l-1}$，在将具体实现之前，我们先看下面这幅图

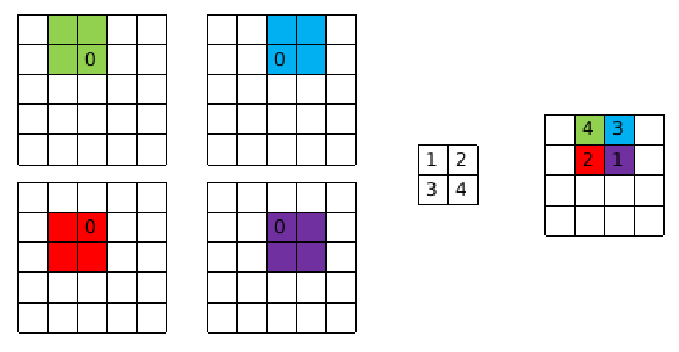
图的左侧表示输入，右侧表示输出。在输入数据中，数字0所标识的位置分别经历了四次卷积过程，分别对输出层的四个位置产生影响，卷积核中的4、3、2、1标识的是其每次参与运算的权重。如果我们现在需要计算0所在位置的误差项，只需要将卷积核中4、3、2、1四个权重与输出层对应位置的误差项进行点积运算即可。这种做法与互相关相同，但是需要注意的是这里的卷积核与之前的不同，是前向传播中的卷积核旋转180度的结果。我们给出输入层的误差项$\delta^{l-1}$的公式
$$
\delta^{l-1}=\delta^{l} * \operatorname{rot} 180\left(W^{l}\right)
$$
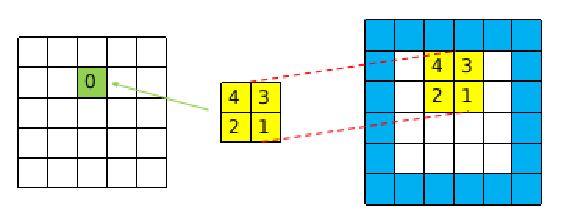
除此之外，由于输出层的尺寸要小于输入层，所以在进行卷积之前需要对输出层进行padding，如下图所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def nexteta(self, grad):
    # 计算卷积输入层的误差项
    n, c, s, _ = grad.shape
    ln, lc, ls, _ = self.param['inputshape']
    pad = math.ceil((self.stride*(ls-1) + self.k_size - s) / 2) 
    grad = self.paddings(grad, pad)
    w = torch.flip(self.w, dims=[2,3]) # 卷积核翻转

    p = (s - self.k_size) // self.stride + 1
    w = w.reshape(lc, self.k_size**2*c)
    im = self.im2col(grad, n, c, s, p)
    eta = torch.matmul(im, w.T).reshape(n, lc, p, p)
    return eta   

def paddings(self, input, pad):
    # padding实现接口
    n, c, s, _ = input.shape
    outshape = pad*2 + s
    out = torch.zeros((n, c, outshape, outshape))
    out[:,:,pad:outshape-pad,pad:outshape-pad] = input
    return out

接下来，我们要对卷积核进行更新。首先我们给出计算公式，
$$
\frac{\partial J(W, b)}{\partial W^{l}}=a^{l-1} * \delta^{l}
$$
其中$a^{l-1}$表示卷积层的输入， $\delta^{l}$表示卷积操作的输出层的误差项。根据前面的描述我们可以知道，$a^{l-1}$是一个$(n, 3, 5, 5)$的矩阵，$\delta^{l}$是$(n, 10, 4, 4)$的矩阵，而我们要求解的卷积核的梯度是$(10, 3, 2, 2)$的矩阵。大致的计算过程是这样的：将$\delta^{l}$视为卷积核，每次取第$i$通道$(n, i, 4, 4)$分别与对应数据的$(n, 3, 5, 5)$的三个通道进行卷积操作，由此可以得到$(n, 3, 2, 2)$，然后对$n$维数据进行求和取平均即得到$(1, 3, 2, 2)$。将此过程进行10次，即可得到卷积核的梯度值，具体代码如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def backward(self, input, grad):
    dw = torch.zeros(self.w.shape)
    db = torch.zeros(self.b.shape)
    n, c, s, _ = grad.shape
    for i in range(self.k_size):
        for j in range(self.k_size):
            cons = input[:,:,i*self.stride:i*self.stride+s,\n 
                         i*self.stride:i*self.stride+s]
            for k in range(c):
                dw[k,:,i,j] = torch.sum(cons * (grad[:, \n
                         k, :, :])[:, None], axis=(0,2,3)) / n
                db = torch.sum(grad, axis=(0,2,3)) / n
    self.w -= self.learning_rate*dw # 更新权重
    self.b -= self.learning_rate*db # 更新偏置
    eta = self.nexteta(grad)
    return eta

池化层

  池化层又称为降采样层，作用是对感受域内的特征进行筛选，提取区域内最具代表性的特征，能够有效地降低输出特征尺度，进而减少模型所需要的参数量。按操作类型通常分为最大池化、平均池化和求和池化，它们分别提取感受域内最大、平均与总和的特征值作为输出，最常用的是最大池化（这里主要介绍最大池化）。

  开始介绍之前，简要说明参数设置情况。输入数据尺寸为$s=4$，通道数为$in_channel=10$，即$ input=(n, 10, 4, 4)$；池化窗口尺寸为$k=2$，池化步幅$stride=2$，根据特征图大小计算公式
$$
p=\frac{s-k}{stride}+1
$$
则池化层输出为$output=(N, 10, 2, 2)$。

前向计算

  与卷积操作相比，池化层的计算较为简单，且池化层不改变通道数量，不包含训练参数。最大池化提取感受域内最大的值作为输出，计算过程如下图所示

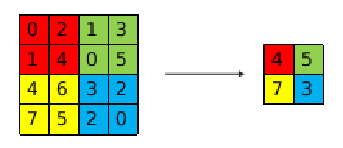
需要注意的是，进行池化操作时需要记录感受域内最大值的位置，在反向传播时会用到，具体代码如下所示（因为需要记录位置，暂时没想到好的解决办法，所以直接用的循环）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def pool(self, input):
    self.param['shape'] = input.shape
    n, c, s, _ = input.shape
    p = (s - self.k_size) // self.stride + 1
    pl = torch.zeros((n, c, p, p))
    index = []
    for i in range(n):
        for j in range(c):
            for k in range(p):
                for z in range(p):
                    inp = input[i,j,k*self.stride:k*self.stride+self.k_size,
                                z*self.stride:z*self.stride+self.k_size]
                    pl[i,j,k,z] = torch.max(inp)
                    ix = torch.where(inp==pl[i,j,k,z])
                    index.append((i,j,k*self.stride+ix[0],z*self.stride+ix[1])) 
                    self.param['index'] = index
    return pl

反向传播

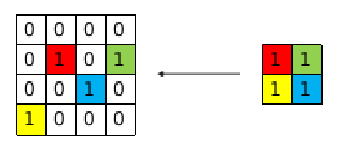
  池化操作的反向传播主要是计算其输入层的误差项。首先我们定义一个全0矩阵，其大小与池化操作输入相同，对于最大池化而言，将池化操作输出层的误差项的值放在之前做前向传播算法得到最大值的位置，如下图所示。

1
2
3
4
5
6
7
def backward(self, input, grad):
    # 反向传播
    grad = grad.reshape(-1)
    eta = torch.zeros(self.param['shape'])
    for i in range(len(self.param['index'])):
    eta[self.param['index'][i]] = grad[i]
    return eta

测试结果

  我们定义了一个简单的卷积神经网络模型，并在FashionMnist做了一组测试。由于在池化层等操作上使用了循环操作，再加上笔记本性能不是特别好，跑了一个epoch，模型在测试集上的预测准确率达到了71.3%，但是花费的时间较长，大概40分钟，整体的代码确实需要做一些优化。

1
2
3
4
5
6
7
8
9
learning_rate = 0.1
network = []
network.append(Convolutional(1,16,5,2,learning_rate=learning_rate))
network.append(ReLU())
network.append(MaxPooling(16,2,2))
network.append(Dense(576,20,learning_rate=learning_rate))
network.append(ReLU())
network.append(Dense(20,10,learning_rate=learning_rate))
network.append(Softmax())

  总的来说，完整实现一个卷积神经网络还是有难度的。整个过程我觉得最难的是理解数据在卷积网络中的流动过程，因为这些数据都是以张量的形式呈现，所以理解起来有些困难。除此之外就是代码的调试，因为其中存在很多细节，一个地方出问题就会对整个结果产生影响。但是，经历这个过程之后，确实对卷积网络有了更多的认识。

坚持原创技术分享，您的支持将鼓励我继续创作！